Để mô tả tính biến thiên (variability) của dữ liệu người ta tính toán các
tham số là: quãng (range), phương sai (variance) và độ lệch chuẩn (standard
deviation).
Quãng (range) là
khoảng khác biệt giữa quan sát có giá trị lớn nhất và quan sát có giá trị nhỏ
nhất.
Range = Max – Min
Trong thực tế, ta
ít khi dùng range để mô tả tính biến thiên bởi vì nó chỉ thể hiện thông tin của
hai giá trị lớn và nhỏ nhất. Vì thế người ta dùng độ lệch (deviation) để mô tả khoảng lệch của từng quan sát so với
giá trị trung bình.
Mỗi quan sát đều có một
deviation, nhận giá trị dương hoặc âm tùy theo vị trí của nó nhỏ hơn hay lớn
hơn giá trị trung bình. Tổng các độ lệch này luôn bằng 0. Vì vậy, người ta phải
tính tổng bình phương của chúng (sum of
squares), ký hiệu là:
Độ lệch chuẩn (standard deviation) là căn bậc hai của phương sai :
Độ lệch chuẩn thể
hiện khoảng lệch tiêu biểu hay là khoảng lệch trung bình của một quan sát so với
giá trị trung bình. Độ lệch chuẩn càng lớn thì dữ liệu càng biến thiên mạnh. Ngoài ra, độ lệch chuẩn vì được tính dựa theo
giá trị trung bình cho nên cũng phản ứng nhạy với giá trị ngoại vi.
Khái niệm bậc tự do
(degrees of freedom)
Giá trị (n-1) như ta thấy ở công thức tính phương sai gọi là bậc tự do của mẫu. Bạn
có thể sẽ thắc mắc vì sao ta lại chia tổng bình phương độ lệch cho cỡ mẫu trừ
đi 1 chứ không phải là cho cỡ mẫu n. Lấy ví dụ rằng khi ta biết giá trị trung
bình của một mẫu là 5, mẫu có 4 quan sát. Khi đó tổng giá trị của mẫu sẽ là 20.
Nếu biết 3 quan sát của mẫu có giá trị lần lượt là 5, 8, 4 thì giá trị còn lại
phải là 3. Nó đã được ấn định ngay khi có ba trong số bốn giá trị của mẫu cho
trước. Khi đó, ta nói mẫu có 3 bậc tự do. Khái niệm này khá khó hiểu, tuy
nhiên, chúng ta chỉ cần nhớ là nó có
liên quan tới tất cả các con số thống kê của mẫu mà ta dùng để suy luận về
thông số của quần thể và bậc tự do luôn bằng cỡ mẫu trừ đi 1.
Một cách diễn giải độ
lệch chuẩn s: Quy Tắc Kinh Nghiệm (The Empirical Rule)
Nếu một phân phối dữ liệu có một chóp đỉnh và có dạng đối xứng
với hình chuông (bell-shaped) thì ta có thể diễn giải s một cách chính xác hơn
như sau:
68% các quan sát nằm trong khoảng 1 độ lệch chuẩn so với giá
trị trung bình, nghĩa là trong khoảng
95% các quan sát nằm trong khoảng 2 độ lệch chuẩn so với giá
trị trung bình, nghĩa là trong khoảng
Đồ thị mô tả quy tắc
kinh nghiệm


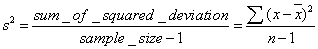

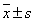



Không có nhận xét nào:
Đăng nhận xét