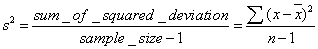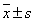TK7. Thống kê mô tả: Đo lường Tính biến thiên của dữ liệu (tt)

Ngoài các tham số như giá trị trung bình và trung vị để đo lường khuynh hướng trung tâm hay độ lệch chuẩn để đo lường tính biến thiên, người ta còn dùng các tham số chỉ vị trí của phân bố. Một vài ví dụ về tham số chỉ vị trí như trung vị (median)- điểm giữa của phân bố; min-max, giá trị nhỏ và lớn nhất của phân bố hoặc z-score- đại lượng cho biết một quan sát lệch khỏi giá trị trung bình bao nhiêu lần độ lệch chuẩn.

Trung vị thực chất là trường hợp đặc biệt của tham số chỉ vị trí có tên gọi là bách phân vị (percentiles). Bách phân vị thứ p (p^th percentile) là vị trí có p phần trăm trên tổng số quan sát nhận giá trị nhỏ hơn hoặc bằng giá trị tại điểm đó ( với điều kiện dữ liệu đã được sắp xếp theo thứ tự từ nhỏ đến lớn). Trung vị là giá trị giữa của quan sát, vì vậy ta còn gọi trung vị là bách phân vị thứ 50 (50^th percentile), nghĩa là có 50% tổng số quan sát nhận giá trị nhỏ hơn hoặc bằng giá trị tại điểm bách phân vị thứ 50.

Một dạng đặc biệt của bách phân vị đó là tứ phân vị (quartiles). Có 3 tứ phân vị:

• Tứ phân vị thứ nhất (first quartile, Q1) tương ứng với bách phân vị thứ 25 (25^th percentile).
• Tứ phân vị thứ hai (second quartile, Q2, hay median) tương ứng với bách phân vị thứ 50 (50^th percentile).
• Tứ phân vị thứ ba (third quartile, Q3) tương ứng với bách phân vị thứ 75 (75^th percentile).

Tứ phân vị được xác định như sau:

•          Sắp xếp dữ liệu theo thứ tự tăng dần
•          Tìm trung vị, đây là Q2
•          Tìm trung vị của dãy số ở dưới Q2 (lưu ý nếu tổng số quan sát là số lẻ thì không tính trung vị trong khoảng này), đây là Q1
•          Tìm trung vị của dãy số ở trên Q2 (lưu ý nếu tổng số quan sát là số lẻ thì không tính trung vị trong khoảng này), đây là Q3

Khoảng tứ phân vị (interquartile range, IQR) là khoảng cách giữa Q1 và Q3.

Công thức tính: IQR= Q3-Q1

Một phương pháp xác định giá trị ngoại biên (potential outlier):

 Ta gọi:

• L (tức lower) là giá trị thấp của biến, L = Q1 – 1,5xIQR
• U (tức upper) là giá trị cao của biến, U = Q3 + 1,5xIQR
• Kết luận: Nếu trong dãy số có số nào thấp hơn L hay cao hơn U thì có thể xem đó là outlier.

Phương pháp kiểm định outlier trên còn gọi là phương pháp phi tham số, ngoài ra còn có phương pháp dựa vào giả định phân phối chuẩn và phương pháp dựa vào số trung vị. Tuy nhiên phương pháp phi tham số là phương pháp phổ biến và cũng dễ ứng dụng nhất, đặc biệt là trong trường hợp dữ liệu không tuân theo luật phân phối chuẩn. 

TK6. Thống kê mô tả: Đo lường Tính biến thiên của dữ liệu

Để mô tả tính biến thiên (variability) của dữ liệu người ta tính toán các tham số là: quãng (range), phương sai (variance) và độ lệch chuẩn (standard deviation).

Quãng (range) là khoảng khác biệt giữa quan sát có giá trị lớn nhất và quan sát có giá trị nhỏ nhất.

Range = Max – Min

Trong thực tế, ta ít khi dùng range để mô tả tính biến thiên bởi vì nó chỉ thể hiện thông tin của hai giá trị lớn và nhỏ nhất. Vì thế người ta dùng độ lệch (deviation) để mô tả khoảng lệch của từng quan sát so với giá trị trung bình.

Độ lệch của một quan sát so với giá trị trung bình là : 

Mỗi quan sát đều có một deviation, nhận giá trị dương hoặc âm tùy theo vị trí của nó nhỏ hơn hay lớn hơn giá trị trung bình. Tổng các độ lệch này luôn bằng 0. Vì vậy, người ta phải tính tổng bình phương của chúng (sum of squares), ký hiệu là:

Phương sai (variance), ký hiệu là s², là trung bình của tổng bình phương các độ lệch :

Độ lệch chuẩn (standard deviation) là căn bậc hai của phương sai :

Độ lệch chuẩn thể hiện khoảng lệch tiêu biểu hay là khoảng lệch trung bình của một quan sát so với giá trị trung bình. Độ lệch chuẩn càng lớn thì dữ liệu càng biến thiên mạnh.  Ngoài ra, độ lệch chuẩn vì được tính dựa theo giá trị trung bình cho nên cũng phản ứng nhạy với giá trị ngoại vi.  

Khái niệm bậc tự do (degrees of freedom)

Giá trị (n-1) như ta thấy ở  công thức  tính phương sai gọi là bậc tự do của mẫu. Bạn có thể sẽ thắc mắc vì sao ta lại chia tổng bình phương độ lệch cho cỡ mẫu trừ đi 1 chứ không phải là cho cỡ mẫu n. Lấy ví dụ rằng khi ta biết giá trị trung bình của một mẫu là 5, mẫu có 4 quan sát. Khi đó tổng giá trị của mẫu sẽ là 20. Nếu biết 3 quan sát của mẫu có giá trị lần lượt là 5, 8, 4 thì giá trị còn lại phải là 3. Nó đã được ấn định ngay khi có ba trong số bốn giá trị của mẫu cho trước. Khi đó, ta nói mẫu có 3 bậc tự do. Khái niệm này khá khó hiểu, tuy nhiên,  chúng ta chỉ cần nhớ là nó có liên quan tới tất cả các con số thống kê của mẫu mà ta dùng để suy luận về thông số của quần thể và bậc tự do luôn bằng cỡ mẫu trừ đi 1.

Một cách diễn giải độ lệch chuẩn s: Quy Tắc Kinh Nghiệm (The Empirical Rule)

Nếu một phân phối dữ liệu có một chóp đỉnh và có dạng đối xứng với hình chuông (bell-shaped) thì ta có thể diễn giải s một cách chính xác hơn như sau:

68% các quan sát nằm trong khoảng 1 độ lệch chuẩn so với giá trị trung bình, nghĩa là trong khoảng 

         

95% các quan sát nằm trong khoảng 2 độ lệch chuẩn so với giá trị trung bình, nghĩa là trong khoảng 

97% các quan sát nằm trong khoảng 3 độ lệch chuẩn so với giá trị trung bình, nghĩa là trong khoảng 

Đồ thị mô tả quy tắc kinh nghiệm  

TK5. Thống kê mô tả: Đo lường khuynh hướng tập trung của dữ liệu

Trong các bài trước, ta đã biết cách phân loại dữ liệu và các loại biểu đồ tương ứng với từng loại biến để thể hiện dữ liệu một cách trực quan.  Bây giờ ta sẽ tiếp tục mô tả dữ liệu bằng cách tìm hiểu khuynh hướng tập trung (central tendency) và tính biến thiên (variability) của chúng. Điều này có nghĩa là ta tìm cách trả lời các câu hỏi như ‘Một quan sát tiêu biểu của dữ liệu có giá trị bao nhiêu?’, ‘Dữ liệu có giá trị nào tương đồng nhau không, nếu khác nhau thì mức độ biến thiên cao hay thấp?’ Để trả lời cho câu hỏi thứ nhất, trong bài này chúng ta sẽ tìm hiểu về khuynh hướng tập trung.

Khuynh hướng tập trung thể hiện qua 3 tham số: trung bình số học (mean), trung vị (median) và số mode.

Số trung bình(mean) được tính bằng cách lấy tổng của tất cả giá trị của các quan sát chia cho tổng số quan sát. Với x là biến số, n là cỡ mẫu, ta có công thức tính số trung bình:

Nếu dữ liệu phân bố lệch thì số trung bình sẽ chuyển động lệch về phía đuôi dài hơn một cách tương đối so với trung vị. Số trung bình bị tác động mạnh bởi các giá trị ngoại vi (outliers). Giá trị ngoại vi là quan sát nằm ở vị trí khá xa so với khuynh hướng chung của toàn bộ dữ liệu.

Trung vị(median) là giá trị chính giữa của dãy giá trị của quan sát sau khi được sắp xếp theo thứ tự từ nhỏ nhất đến lớn nhất. Nếu tổng số quan sát là số lẻ thì trung vị là giá trị ở giữa của dãy số. Nếu tổng số quan sát là số chẵn thì trung vị là trung bình cộng của hai giá trị nằm chính giữa dãy số.

So với số trung bình, trung vị ít bị ảnh hưởng bởi giá trị ngoại vi. Vì vậy trong trường hợp dữ liệu phân bố lệch (highly skewed) thì trung vị sẽ cho thông tin chính xác hơn. Tuy nhiên, trường hợp cỡ mẫu nhỏ và biến rời rạc, tính kém nhạy của trung vị lại là một bất lợi cho việc mô tả dữ liệu, khi đó ta nên sử dụng số trung bình để có thể phản ánh được tất cả các giá trị của quan sát. Đôi khi nếu biến rất rời rạc và có nhiều hơn 2 nhóm thì cách hữu ích nhất là tính tỉ lệ phần trăm (tần suất) của các giá trị thay vì tính mean hay median. Trong thực tế thì thường cả mean và median đều có ích và đều được tính toán bởi các hàm có sẵn trong các phần mềm thống kê.

So sánh số trung bình và trung vị dựa theo hình dạng của phân bố:

•          Nếu phân bố đối xứng hoàn toàn(perfectly symmetric) thì số trung bình bằng trung vị.
•          Nếu phân bố lệch trái (left-skewed) thì số trung bình nhỏ hơn trung vị.
•          Nếu phân bố lệch phải (right-skewed) thì số trung bình lớn hơn trung vị.

Mode (hay modal frequency) là giá trị lặp lại nhiều lần nhất trong mẫu, thường được dùng để mô tả một nhóm hoặc giá trị có tần số cao nhất của biến phân loại hoặc biến rời rạc. 

TK4. Các loại biểu đồ (tt): Hình dạng của phân bố

Khi tìm hiểu về phân bố của một biến định lượng được thể hiện qua bảng tần số hoặc đồ thị, ta đặt những câu hỏi sau: 

·         Xu hướng chung (overall pattern) là gì? Dữ liệu bó lại thành cụm (cluster) hay có khoảng trống (gap) qua đó có 1 hay vài quan sát nằm cách xa khỏi tất cả các quan sát còn lại?

·         Dữ liệu có một chóp (unimodal) hay hai chóp (bimodal)? (Trường hợp dữ liệu bimodal xảy ra khi lấy ý kiến về một vấn đề gây tranh cãi với số lượng ý kiến gần như ngang nhau ở mỗi bên,c hẳng hạn như nạo phá thai, nên hay không?)

·         Phân bố có hình dạng đối xứng (symmetric) hay nghiêng về một bên (skewed)? Phân bố nghiên về bên trái nếu đuôi bên trái dài hơn đuôi bên phải và ngược lại. 

**** Theo bạn, đồ thị của các biến sau có hình gì?

-Thu nhập

-IQ

-Tuổi thọ

TK3. Thống kê mô tả: Các loại biểu đồ

Đối với biến phân loại, ta có thể dùng biểu đồ hình bánh (pie chart) hoặc biểu đồ thanh (bar graph). Biểu đồ thanh dễ đọc và cho nhiều thông tin hơn so với biểu đồ bánh. Ví dụ khi muốn mô tả sự khác biệt rất nhỏ giữa từng nhóm hoặc muốn thể hiện độ lệch chuẩn của mỗi nhóm, ta nên chọn biểu đồ thanh.

Pareto chart là biểu đồ thanh trong đó ta sắp xếp các nhóm (thanh) theo thứ tự tần số giảm dần, tức cột cao nhất đến cột thấp nhất. Biểu đồ này phác họa nguyên lý Pareto: một vài nhóm chiếm tần số cao nhất trong tổng số lượng quan sát.

Đối với biến định lượng, có 3 loại biểu đồ đó là: dot plot, stem-and-leaf plot và histogram.

Dot plot: Bao gồm một đường thẳng nằm ngang, trên đó thể hiện các giá trị nhận được của biến. Tiêu đề thanh là tên biến. Mỗi quan sát sẽ được thể hiện bằng 1 dấu chấm tròn ngay bên trên của giá trị tương ứng.  

Stem and leaf plot: Sắp xếp dữ liệu theo thứ tự từ nhỏ đến lớn. Mỗi quan sát được thể hiện bởi một stem và 1 leaf. Thông thường cột stems sẽ bao gồm toàn bộ chữ số, riêng chữ số cuối cùng nằm ở cột leaves.

Cả hai biểu đồ này có điểm mạnh là có thể thể hiện rõ giá trị của từng quan sát, phù hợp để mô tả dữ liệu có cỡ mẫu nhỏ và có thể biểu diễn hình dạng (shape) của phân bố.

Histogram: là biểu đồ trong đó có các thanh (bar) đặt liên tiếp, sát cạnh nhau để diễn tả tần số hoặc tần số tương đối (%) của một biến số. 

*Nguồn biểu đồ: Statistics, The Art and Science of Learning from data_3e, Agresti & Franklin

TK2. Thống kê mô tả: Phân loại dữ liệu

Trong thống kê, người ta nói nhiều về tính biến thiên bởi vì đây là một yếu tố cốt lõi của môn khoa học này. Để biểu thị tính đa dạng của dữ liệu (data), ta dùng các biến số (variables). Biến số là bất kỳ đặc tính nào mà ta quan sát thấy được trong một nghiên cứu và biến số có thể nhận nhiều giá trị khác nhau. Thuật ngữ variable tự nó cũng cho thấy tính chất biến thiên của dữ liệu. Ví dụ, GPA, lượng mưa trung bình, GDP đầu người là các biến số bởi vì chúng thay đổi tùy từng đối tượng như là sinh viên, thành phố, quốc gia. Có hai loại biến là: biến phân loại và biến định lượng.

Biến phân loại (categorical) là biến có giá trị thuộc vào một nhóm nào đó và nó không có giá trị định lượng. Ví dụ tình trạng hôn nhân, nơi sinh, ngành học là các biến phân loại. Để mô tả biến phân loại, người ta tính tần số hay phần trăm của từng nhóm và của nhóm cao nhất (modal category). Ví dụ như, có bao nhiêu phần trăm sinh viên tốt nghiệp ngành tâm lý mỗi năm? 

Biến định lượng (quantitative) là biến diễn tả các mức độ cao, thấp của dữ liệu. Ví dụ GPA, thu nhập, số con trong gia đình là các biến định lượng. Để mô tả biến phân loại, người ta tìm hiểu tính trung bình (center) và tính biến thiên (varibility) của chúng. Ví dụ như, GPA trung bình của sinh viên năm cuối là bao nhiêu? Có sự dao động lớn giữa từng năm học không?

Biến định lượng có thế là biến liên tục (continuous) nếu nó có các giá trị số liên tiếp nhau kéo dài vô hạn và tạo thành một khoảng hoặc biến rời rạc (discrete) nếu các giá trị của nó là những con số rời nhau và có hạn. 

Phương pháp phân tích dữ liệu sẽ phụ thuộc vào loại dữ liệu mà ta cần nghiên cứu. Vì vậy, ta cần hiểu rõ cách phân loại biến.

Bảng tần số (frequency table)

Tần số là số lần biến nhận một giá trị nào đó. Tỉ lệ (proportion) là tần số được diễn tả một cách tương đối, được tính bằng cách lấy tần số chia cho tổng số quan sát. Tỉ lệ phần trăm (percentage) là tỉ lệ được nhân lên cho 100. Tỉ lệ và tỉ lệ phần trăm được gọi là tần số tương đối (relative frequencies) và được dùng để mô tả các nhóm của một biến phân loại.

Bảng tần số là bảng liệt kê các giá trị của một biến và tần số của chúng. Nhóm có tần số cao nhất của một biến phân loại gọi là model category, còn giá trị cao nhất của một biến định lượng gọi là mode. 

TK1. Giới thiệu về thống kê*

*Tài liệu tham khảo chính của loạt bài thống kê cơ bản này lấy từ quyển Statistics - The Art and Science of Learning from Data của Agresti và Franklin, NXB: Pearson.
Người biên soạn: Phạm Thị Thủy Tiên
-----

Một cách đơn giản nhất, ta có thể hiểu thống kê là một môn khoa học và cũng là một môn nghệ thuật của việc học từ dữ liệu. Học ở đây có nghĩa là thu nhận lấy kiến thức về thế giới xung quanh, lý giải các mối quan hệ phức tạp trong cái thế giới tương đối ấy và áp dụng những hiểu biết đó để làm cho thế giới trở nên tốt đẹp hơn.

Khác với các triết gia, những người dùng tư duy từ bộ óc của họ để tìm ra những câu trả lời cho những thắc mắc của con người về thế giới, các nhà thống kê học trả lời những câu hỏi ấy bằng dữ kiện thu được từ chính thế giới bên ngoài. Tuy cách tiếp cận là khác nhau, nhưng cả hai đều có cùng mục đích, đó là tìm kiếm chân lý.

Thống kê là một môn học có tính ứng dụng cao, có thể thấy trong rất nhiều ngành khoa học như y khoa, kinh tế, tâm lý, xã hội và cả chính trị. Vì vậy, hiểu biết về thống kê không chỉ cần thiết cho nhà khoa học mà còn có lợi cho chúng ta trong việc nâng cao năng lực phán đoán và khả năng ra quyết định trong đời sống hằng ngày cũng như trong công việc.

Có 3 chủ đề chính trong thống kê, đó là:

• Thiết kế và tiến hành nghiên cứu để thu thập dữ liệu (research design)
• Mô tả, phân tích dữ liệu (descriptive statistics)
• Suy luận từ dữ liệu (inferential statistics)

Một khái niệm cơ bản trong thống kê là mẫu (sample). Mẫu là một số lượng đại diện lấy từ quần thể mà ta chọn để tiến hành nghiên cứu. Ta dùng thống kê mẫu (sample statistics) để ước lượng về các thông số của quần thể (population parameters).

Lấy mẫu ngẫu nhiên (random sampling) là cách chọn mẫu trong đó mỗi đối tượng có cùng khả năng được chọn để quan sát hoặc thí nghiệm. Đây là yêu cầu đầu tiên và tiên quyết để có được một thiết kế nghiên cứu tốt.